Fungsi trigonometri merupakan suatu fungsi yang grafiknya berulang secara terus menerus dalam periode tertentu. Fungsi dari periode itu sendiri merupakan suatu jarak antara dua puncak/lembah atau jarak antara awal puncak dan akhir lembah. Selain itu, terdapat amplitudo yang merupakan setengah dari selisih nilai maksimum dan minimum dari suatu fungsi. Rumus amplitudo sebagai berikut:

Fungsi trigonometri sederhana meliputi fungsi sinus, fungsi cosinus dan fungsi tangen. Masing-masing fungsi tersebut dijelaskan dalam bentuk grafik baku fungsi trigonometri seperti berikut:
- Grafik Fungsi Sinus, y = sin x
Nilai dari sinus adalah -1 ≤ sin (x) ≤ 1

- Grafik Fungsi Cosinus, y = cos x

- Grafik Fungsi Tangen, y = tan x


Fungsi trigonometri memiliki nilai minimum dan maksimum, cara menentukannya dapat menggunakan metode grafik dan melalui rumus. Metode grafik dengan cara menggambarkan grafiknya, titik puncak pada bukit adalah nilai maksimum sedangkan titik terendah pada lembah adalah nilai minimum. Selain dengan grafik, nilai maksimum dan nilai minimum dapat ditentukan dengan rumus sebagai berikut:

1. Melukis grafik fungsi sinus menggunakan tabel
Adapun langkah-langkahnya adalah sebagai berikut.
a. Gunakan nilai perbandingan trigonometri untuk sudut istimewa dengan sudut relasi sebagai x.

b. Melengkapi nilai pada tabel, lalu tulis pasangan koordinat titik-titiknya dalam radian atau derajat.

c. Lukis titik tersebut dalam koordinat kartesius yang sesuai.

d. Lukis kurva melalui titik-titiknya.

2. Melukis grafik fungsi kosinus menggunakan tabel
Sama seperti grafik fungsi sinus, untuk kosinus kamu bisa menentukan terlebih dahulu nilai kosinus sudut-sudut istimewanya.

Dengan demikian, diperoleh grafik berikut ini.

3. Melukis grafik fungsi tangen menggunakan lingkaran satuan
Jari-jari lingkaran satuan yang diperpanjang sampai memotong sumbu-y, akan menghasilkan gambar berikut.

Dari gambar di atas, kamu bisa mendapatkan beberapa nilai tangen berikut.

Nilai di atas menunjukkan bahwa nilai tangennya adalah panjang ruas garis dari titik O sampai ke titik potong jari-jari yang terkait sudut, misalnya sudut x. Untuk melukis grafik fungsi tangen, kamu bisa melalui titik potongnya, dengan ruas atas bertanda positif dan ruas bawah bertanda negatif.

Grafik Fungsi Trigonometri
Secara umum, grafik fungsi trigonometri dibagi menjadi tiga, yaitu sebagai berikut.
1. Grafik fungsi sinus (y = a sin bx, x ∈ [0o, 360o])
Grafik fungsi sinus, y = a sin bx, x ∈ [0o, 360o] memiliki bentuk gelombang bergerak yang teratur seiring pergerakan x. Perhatikan gambar berikut.

Berdasarkan grafik di atas, diperoleh sifat-sifat berikut.
- Simpangan maksimum gelombang atau yang biasa disebut amplitudo adalah 1. Simpangan gelombang adalah jarak dari fungsi x ke puncak gelombang.
- Gelombang memiliki periode satu putaran penuh.
- Grafik y = sin x memiliki nilai ymaks = 1 dan ymin = -1.
- Titik maksimum gelombang adalah adalah (90o, 1) dan titik minimumnya (270o, -1).
Jika persamaan fungsi trigonometrinya diubah menjadi y = a sin x dengan a = 2, diperoleh grafik berikut.
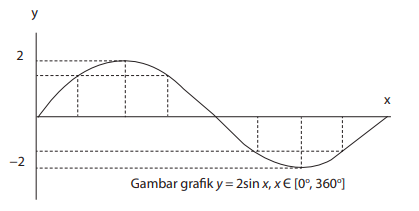
Perubahan nilai a mengakibatkan perubahan amplitudo gelombang. Nah, jika persamaan fungsinya diubah menjadi y = sin bx dengan b = 2, grafiknya akan menjadi seperti berikut.

Artinya, perubahan nilai b mempengaruhi jumlah gelombang yang terbentuk. Pada grafik fungsi y = sin 2x terbentuk 2 buah gelombang.
2. Grafik fungsi kosinus (y = cos 2x, x ∈ [0o, 360o])
Pada dasarnya, grafik fungsi kosinus sama dengan grafik fungsi sinus. Hal yang membedakan adalah grafik fungsi sinus dimulai dari y = 0, sedangkan grafik fungsi kosinus dimulai dari y = 1. Perhatikan grafik berikut.
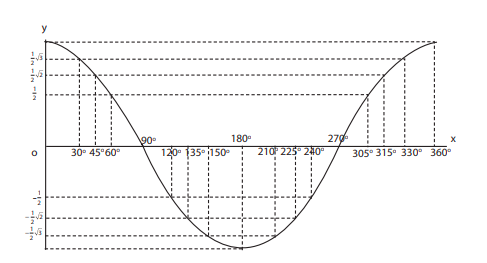
Jika persamaan fungsinya diubah menjadi y = cos 2x, grafiknya menjadi seperti berikut.

Grafik di atas menujukkan adanya dua buah gelombang yang bergerak dari y = 1.
3. Grafik fungsi tangen (y = tan x, x ∈ [0o, 360o])
Adapun ketentuan yang berlaku pada fungsi tangen adalah sebagai berikut.
- Saat x -> 90o dan x -> 270o (dari kanan), nilai y = tan x menuju tak terhingga.
- Saat x -> 90o dan x -> 270o (dari kiri), nilai y = tan x menuju negatif tak terhingga.
Berikut ini contoh grafiknya.

Jika fungsi tangen diubah menjadi y = tan 2x, x ∈ [0o, 360o] grafiknya menjadi seperti berikut.

Untuk mengasah pemahamanmu tentang grafik fungsi trigonometri, simak contoh soal berikut.
Contoh Soal 1
Perhatikan grafik fungsi berikut.
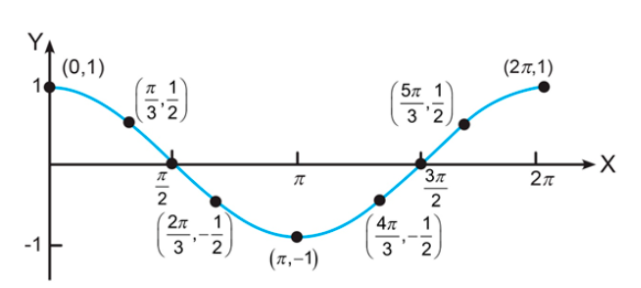
Grafik fungsi tersebut merupakan grafik fungsi jenis apa?
Pembahasan:
Jika diperhatikan, grafik tersebut dimulai dari titik (0,1) dan mempunyai periode satu putaran 0 ≤ x ≤ 2π.
Dengan demikian, grafik fungsi tersebut adalah grafik fungsi cos, yaitu y = cos x. Untuk meyakinkan, coba lihat salah satu titiknya.

Jadi, grafik fungsi tersebut merupakan grafik fungsi y = cos x untuk 0 ≤ x ≤ 2π.
Contoh Soal 2
Lukislah grafik fungsi y = 2 cos 2x, x ∈ [0o, 360o]
Pembahasan:
Untuk menentukan bentuk grafiknya, gunakan tabel trigonometri sudut istimewa.

Dengan demikian, grafik fungsi y = 2 cos 2x, x ∈ [0o, 360o] adalah sebagai berikut.

Contoh Soal 3
Hitunglah nilai maksimum dan minimum fungsi y = cos (x – 30), x ∈ [0o, 360o]. Kemudian, lukislah grafik fungsinya.
Pembahasan:
Berdasarkan tabel trigonometri untuk sudut istimewa, diperoleh:

Berdasarkan tabel di atas, nilai maksimum dari fungsi y = cos (x – 30), x ∈ [0o, 360o] adalah 1 dan nilai minimumnya adalah –1. Untuk lebih jelasnya, simak grafik fungsi berikut.






Comments